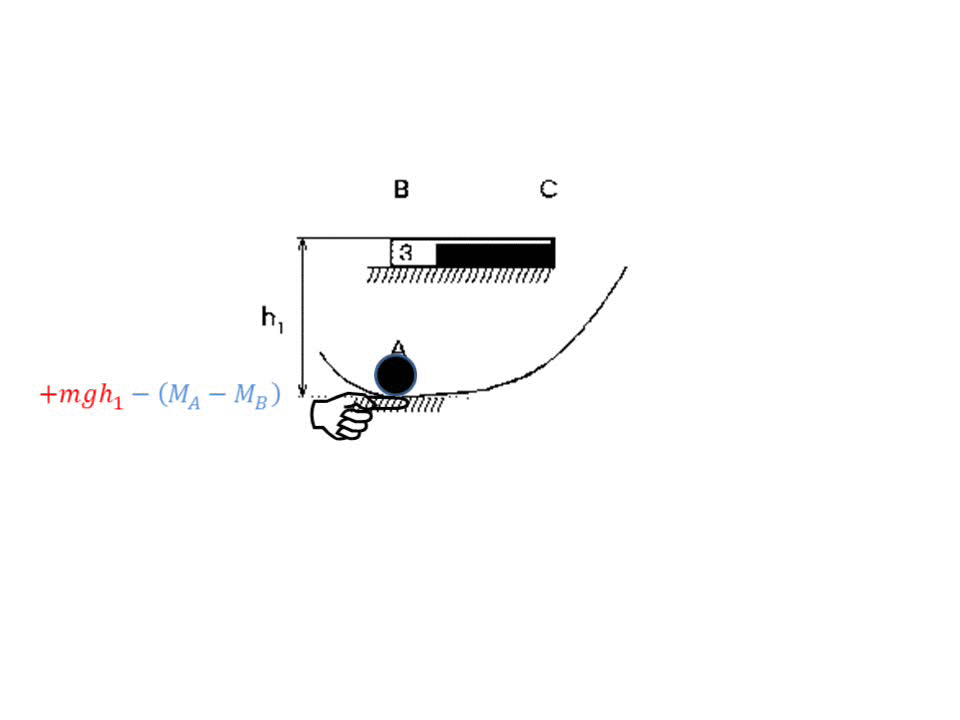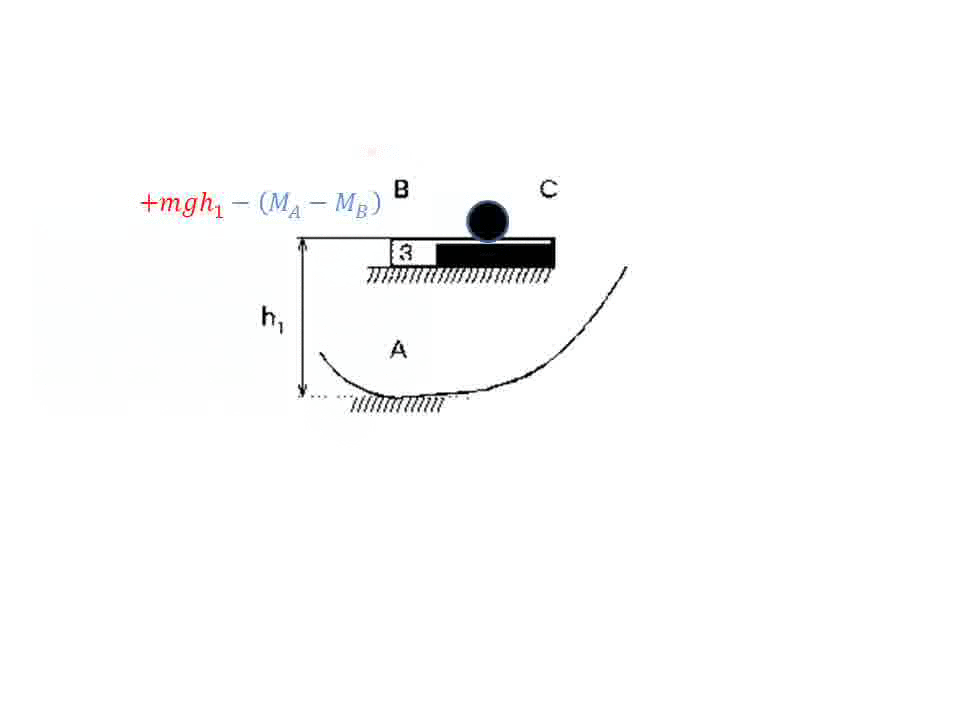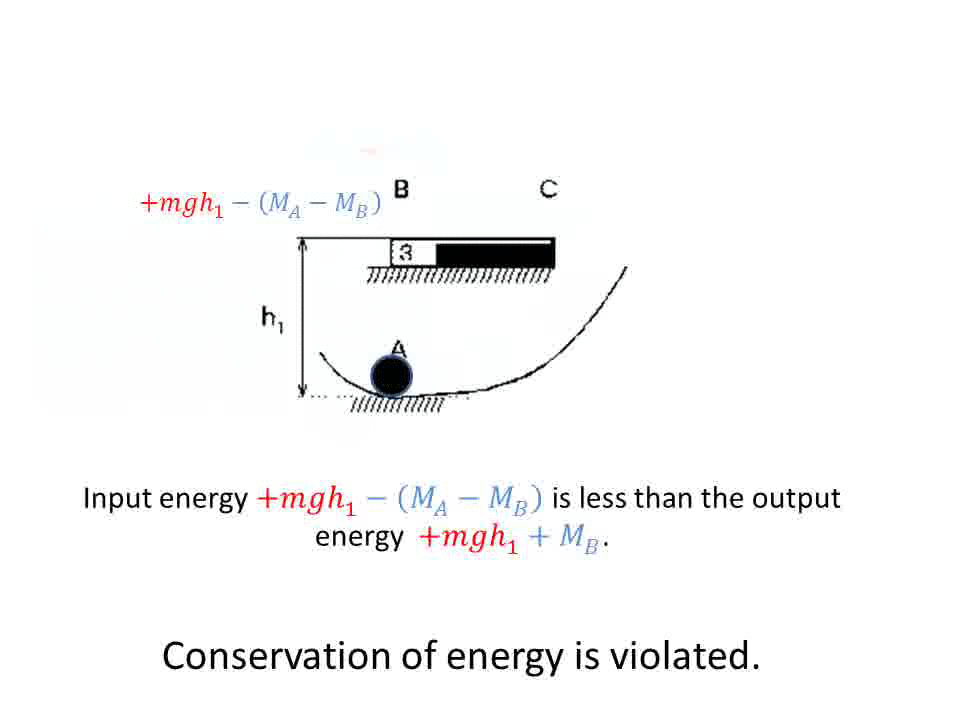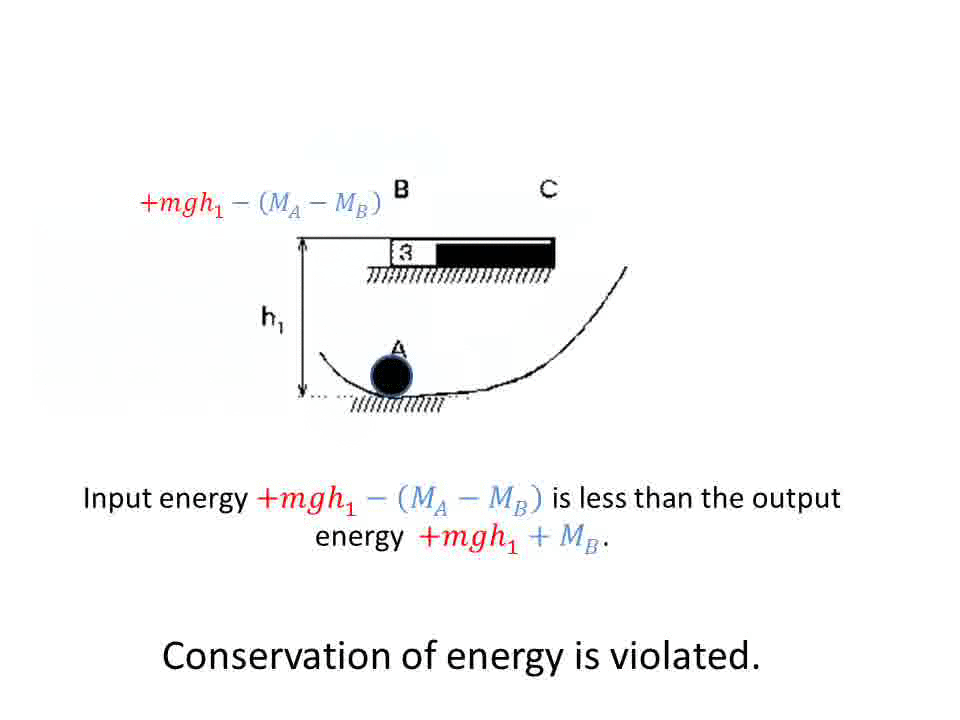
Disobeying Conservation of Energy in Electrical
Systems
__________
It has not been recognized so far that conservation
of energy (CoE) can be violated in classical physics on a macroscopic
level. Clearly, such violation can have a far-reaching direct practical
application because it would supply unlimited amount of energy without
the need to extract it from any preliminary existing energy reservoir.
Also, production of energy as a result of CoE violation need not result
in a self-sustaining, perpetual motion machine, whereby the excess energy
produced at the output is fed back into the input to maintain the working
of the machine, but may be produced in portions for further utilization.
Such possibilities to violate CoE are demonstrated here for the first
time. It is to be understood that while this invention is a generator
of free energy (excess energy), it is in fact the first scientifically
sound proof for the reality of free energy, that in no way makes it akin
to a perpetual motion machine.
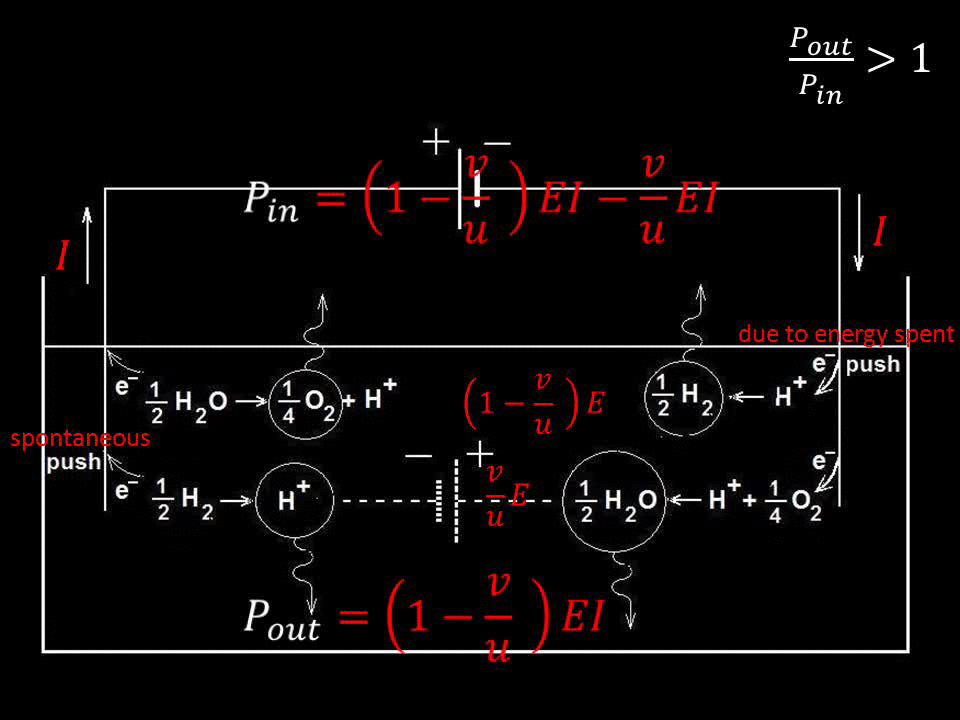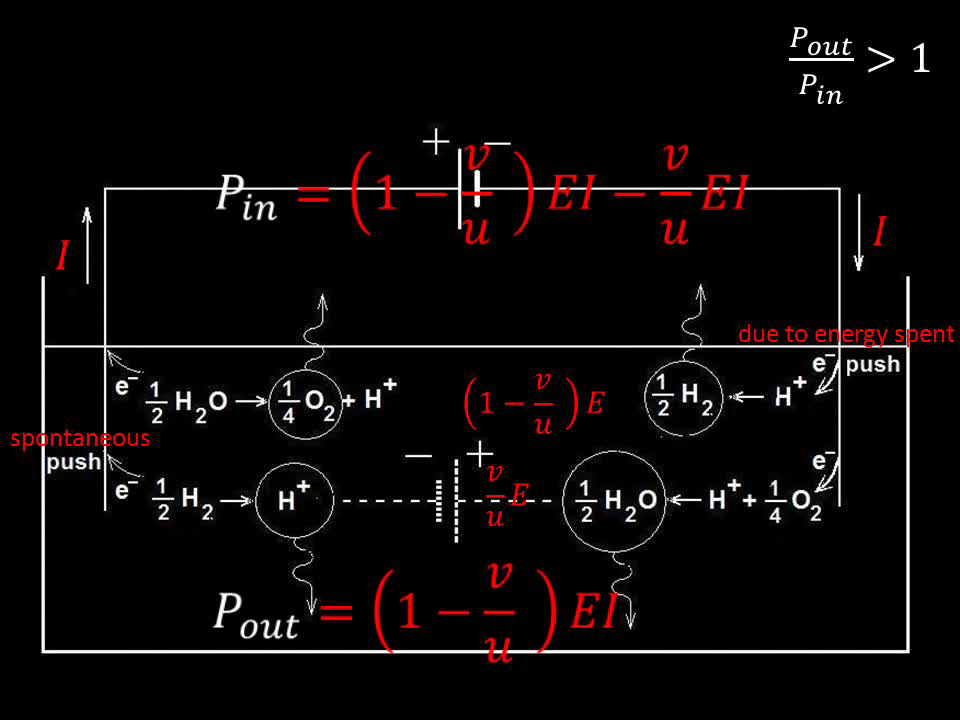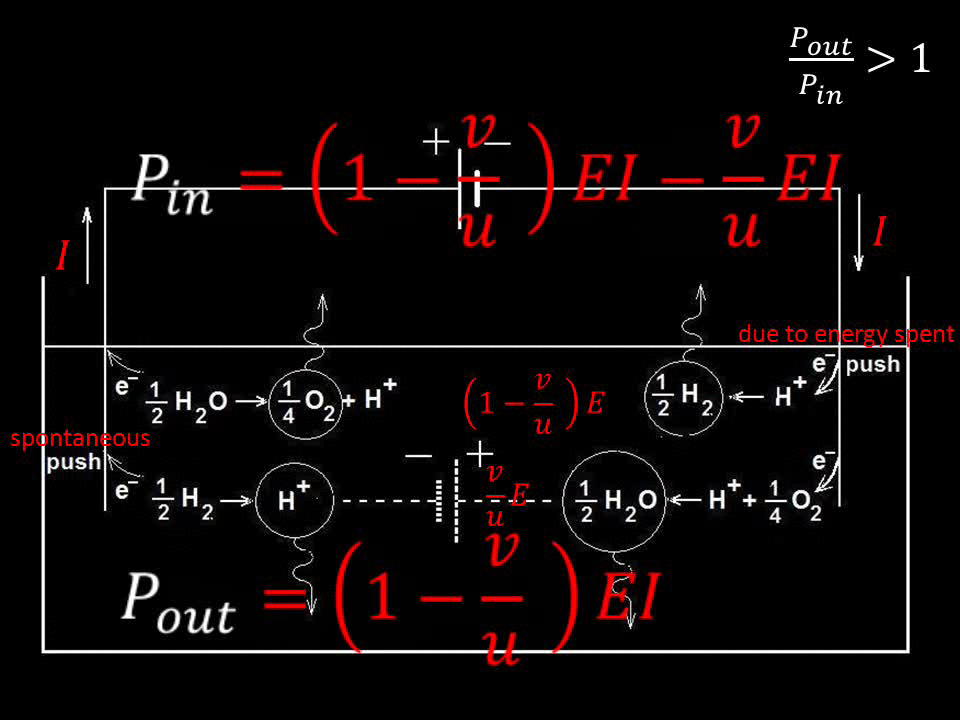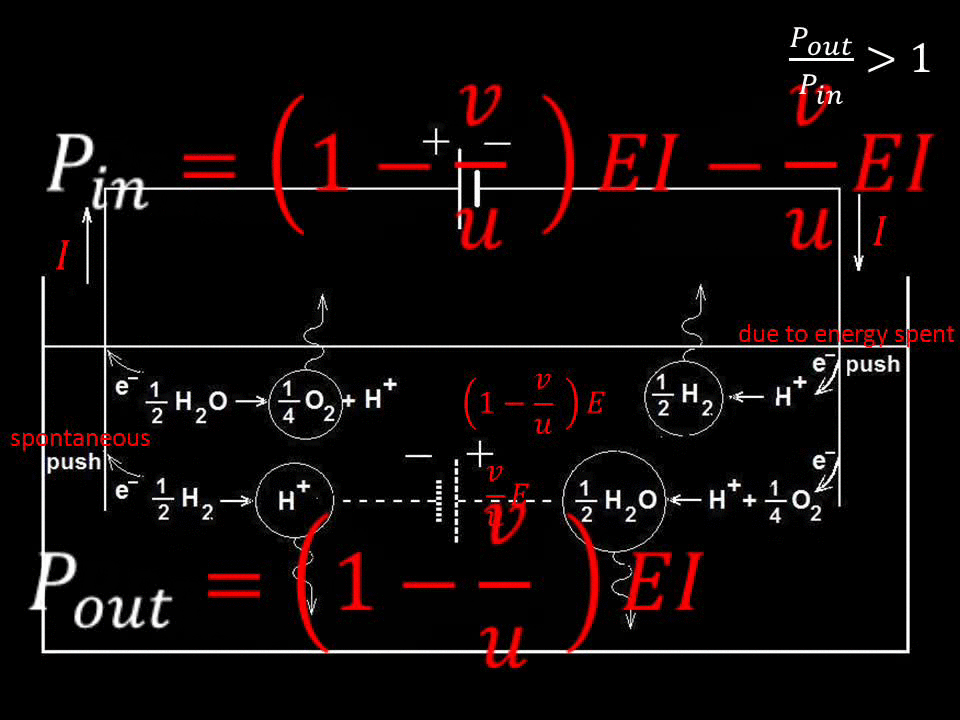
Shown below in more detail is an instance of disobeying conservation of
energy, when alternating voltage is applied to a resistor and a capacitor
connected in series, shown schematically in the expression derived by him
in his founding paper:
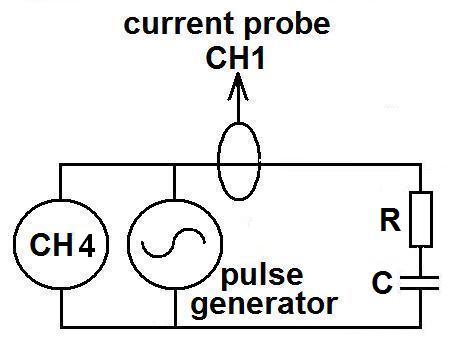
Fig.1
Because it is crucial to prove that violation of CoE
is real, we discuss here the simplest possible illustration, ignoring
details of experimental nature, without losing the rigor needed for such
proof. Of course, a real practical experiment to implement the method
described herein of disobeying CoE, has been carried out and can be carried
out at once by anyone skilled in the art. Furthermore, experimental details
may only cause confusion in some readers because it is usual to deal with
root mean square (rms) values when calculating electric power when alternating
voltage is applied, while the method described herewith uses the more
accurate integral method to calculate power and not the less accurate
method using rms values. Also, many times, experimental details invoke
unjustified objections connected with parasitic inductances and capacitances,
calibration of probes, floating zeroes of the observed signal and many
other unjustified objections, which unnecessarily distract from the essence
of the presented discovery.
The violation of energy conservation observed here
is due to two asymmetries between current and voltage in the system
described here. These two asymmetries are inherent in the theory of electricity.
The first asymmetry, inherent in the theory of electricity,
concerns the phase difference between the applied alternating voltage
V(t) and corresponding current I(t) in an electric circuit
such as the one shown schematically in the Fig.1.
The asymmetries are due to the presence of a capacitor,
causing the relationship between voltage and current to no longer obey
Ohm's law 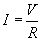 .
Current now is the first time-derivative of voltage, .
Current now is the first time-derivative of voltage, 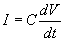 ,
where C is a constant. ,
where C is a constant.
In our mentioned effort to make things simple, without
losing the rigor in displaying this new discovery of violation of CoE,
we illustrate the sinusoidal voltage applied to the RC-circuit by sin
(t) and the current resulting from this voltage by its time-derivative
cos (t). For simplicity, we will consider the resistance R
as negligible. Just as in almost any standard text1-4, the
current is leading the voltage and the phase-shift is 90o. It must be noted that the mentioned natural phase-shift
between I(t) and V(t) in an RC-circuit, seen in every college
level textbook, is of magnitude exactly as much as
is 90o. It must be noted that the mentioned natural phase-shift
between I(t) and V(t) in an RC-circuit, seen in every college
level textbook, is of magnitude exactly as much as 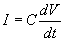 determines,
having a value of determines,
having a value of 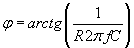 ,
indelibly connected with the concrete RC-circuit under the conditions
at hand. Any deviation of this phase shift ,
indelibly connected with the concrete RC-circuit under the conditions
at hand. Any deviation of this phase shift 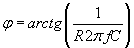 ,
strictly set by the concrete parameters; namely, resistance R,
capacitance C and frequency f, is an immediate sign of CoE
violation, as will be demonstrated herewith. This natural mutual disposition
of current and voltage, having phase-shift ,
strictly set by the concrete parameters; namely, resistance R,
capacitance C and frequency f, is an immediate sign of CoE
violation, as will be demonstrated herewith. This natural mutual disposition
of current and voltage, having phase-shift 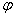 ,
can also be demonstrated in an actual laboratory experiment with an oscilloscope,
measuring the voltage and current of an RC-circuit. ,
can also be demonstrated in an actual laboratory experiment with an oscilloscope,
measuring the voltage and current of an RC-circuit.
The phase-shift  ',
discussed below, giving rise to the violation of CoE, differs from the
natural phase-shift ',
discussed below, giving rise to the violation of CoE, differs from the
natural phase-shift  ,
just mentioned. ,
just mentioned.
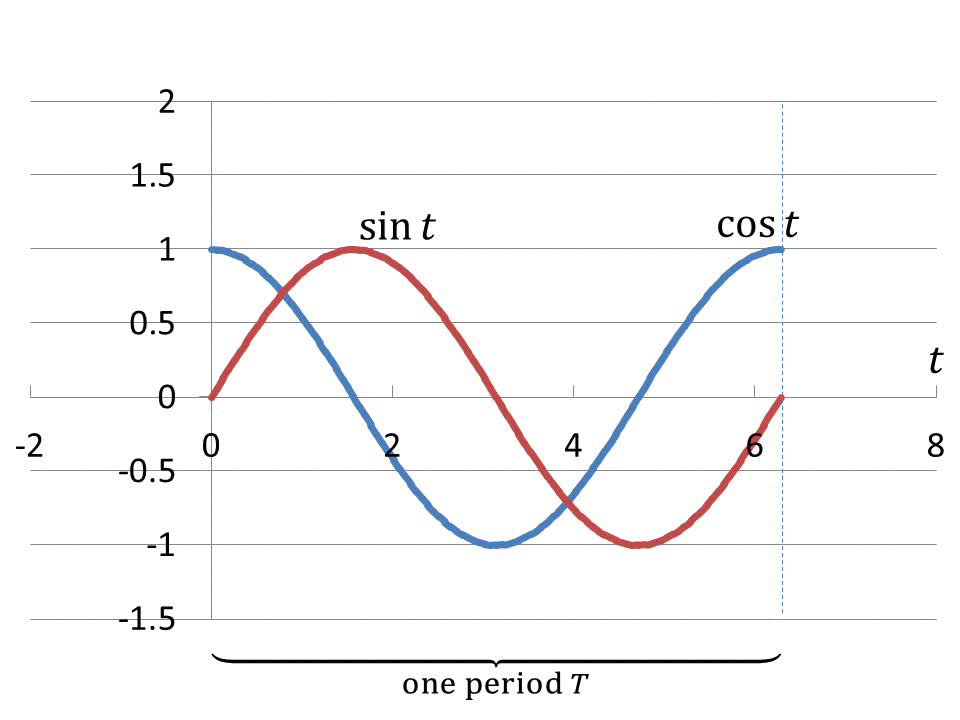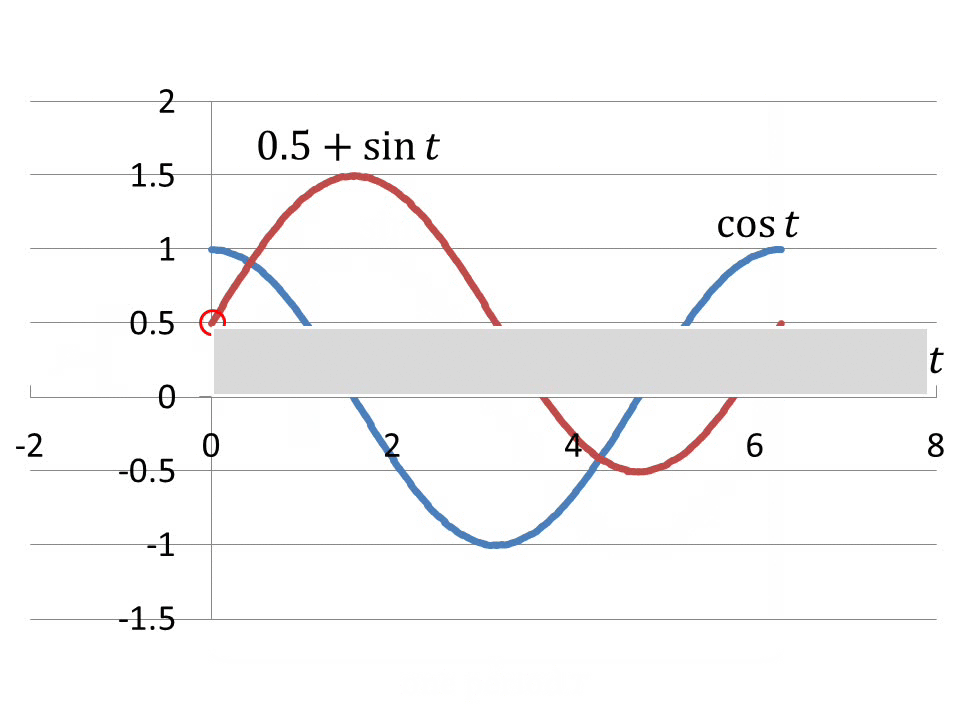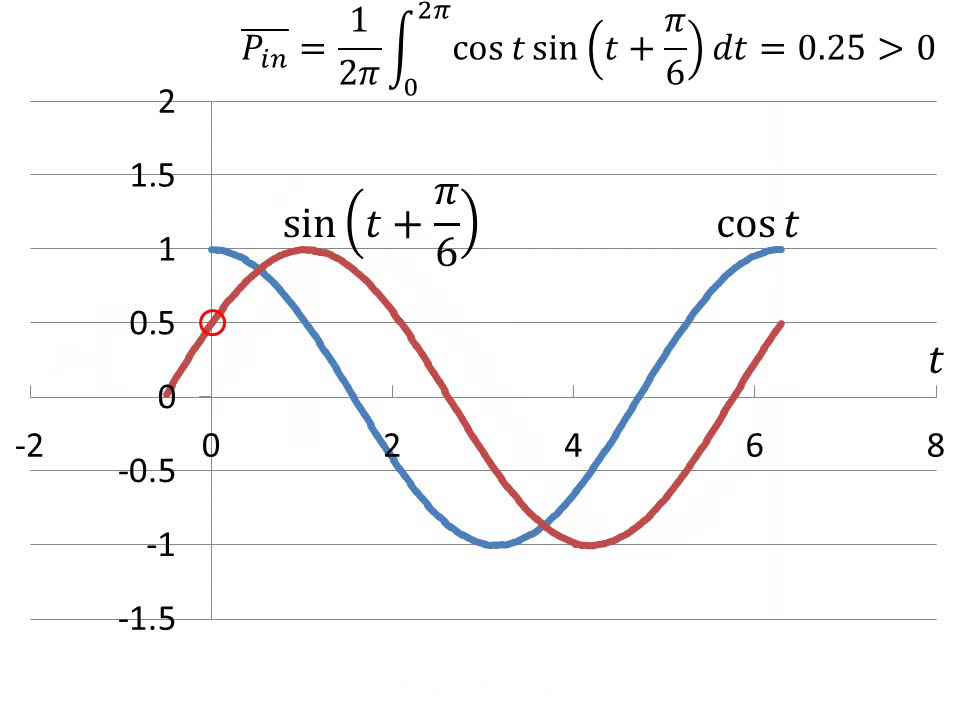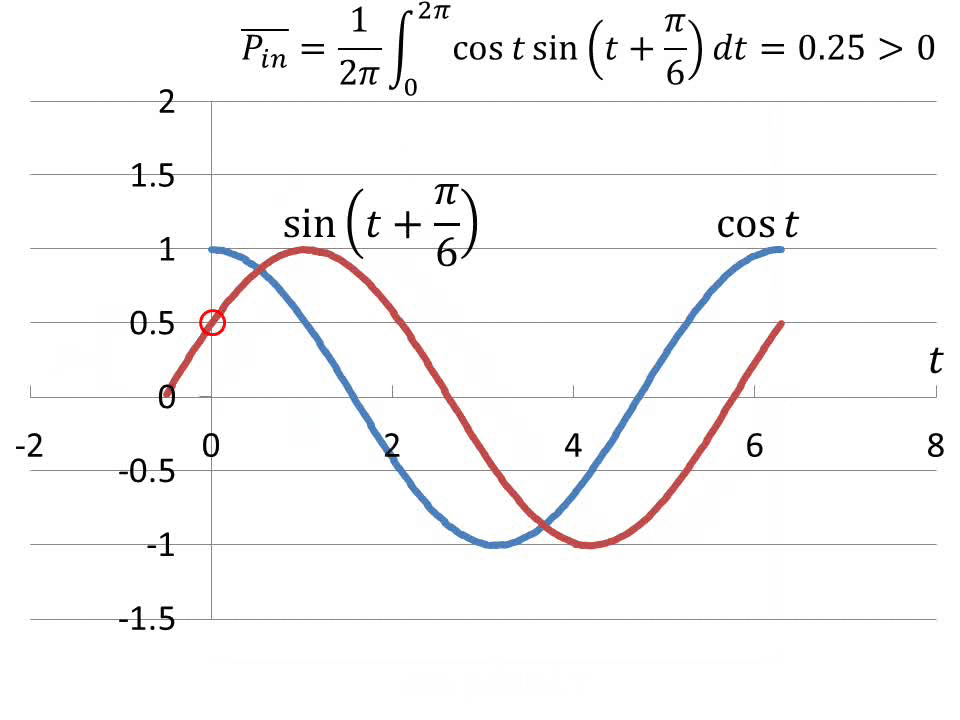
The fact that, due to the presence of a capacitor,
current is the first derivative of voltage, leads to the second asymmetry,
inherent in the theory of electricity; namely, voltage with any added
constant voltage offset invokes the same current without offset. The constant
voltage offset has no contribution to the current. As an illustration,
observe that both curves 1 and 3 in Fig.2 and Fig.3 give rise to the exact
same current, curve 2.
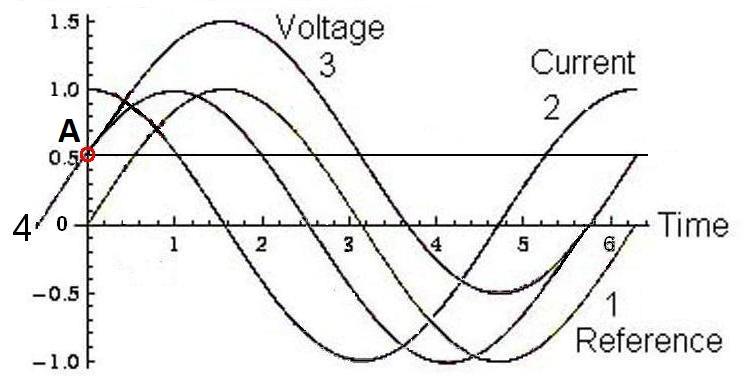
Fig.2
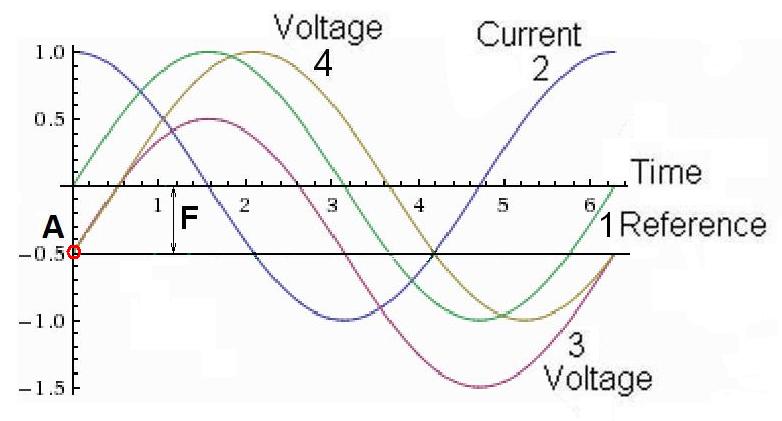
Fig.3
These two inherent asymmetries combined, whose importance
for the power balance has not been recognized thus far, determine the
conditions in electrical systems for disobeying conservation of energy,
with its far-reaching consequences. Revealing of the CoE violation itself,
however, occurs only after understanding exactly how these two inherent
asymmetries affect the determination of input power so that it is correctly
determined.
First, observe voltage with no offset, which standard
texts usually discuss (curve 1 in Fig.2 and Fig.3). Here, the integral
of the voltage times current over the entire period, comprising the input
energy throughout this period, is zero. Respectively, the quotient of
that input energy and the period, comprising the average input power 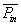 ,
is also zero. ,
is also zero.
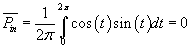 (1)
(1)
The physical meaning of this result is cited in the
standard texts as a proof that conservation of energy is obeyed in electrical
systems; that is, within the period 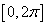 ,
energy is given to the capacitor twice, in the first and third quarters
of the period, resulting in the capacitor acquiring energy of the electric
field, that energy of the electric field being returned back to the generator
also twice within the period, in the second and fourth quarters,in exactly
the same quantities as the energy put in. ,
energy is given to the capacitor twice, in the first and third quarters
of the period, resulting in the capacitor acquiring energy of the electric
field, that energy of the electric field being returned back to the generator
also twice within the period, in the second and fourth quarters,in exactly
the same quantities as the energy put in.
The standard texts, however, incorrectly generalize
the conclusion regarding the obeying of conservation of energy to apply
also to alternating voltage with constant voltage offset.
Unrecognized so far is the fact that the physical
picture regarding conservation of energy changes when a constant voltage
offset is added to the sinusoidal voltage (cf. curve 3 in Fig.2 and Fig.3).
Superficially, it may appear that the average input
power for the period is to be calculated by a similar integral, summing
up the instantaneous products of voltage and current, and then dividing
this integral by the period.
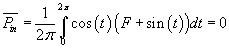 (2)
(2)
This integral would yield zero as well and one may
conclude incorrectly that conservation of energy is also valid when there
is constant offset added to the sinusoidal voltage.
Observe, however, that most voltage values in eq.(2),
used to calculate momentary input power, contain a constant voltage offset
part, which gives rise to no current; that is, gives rise to no power.
Therefore, inclusion of such non-power invoking voltage deforms the calculated
momentary power value, making it incorrect.
To understand the above, imagine that just the constant
voltage offset F = 0.5V in Fig.2 is applied to the capacitor. Aside
from the initial charging current that has occurred a long, long time
ago, there will be no current flowing through capacitor, therefore, no
power will be input throughout the time F is applied.
When now a voltage ripple is invoked (curve 3 in Fig.2),
causing current, it should be obvious that the input power is only due
to the product of current and the voltage of the undulation. The input
power is only due to the product of the current and the wavy part of the
voltage. The underlying constant part of the voltage F = 0.5V is
not participating in the formation of the input power
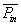 . .
To help us understand the concept, we now imaginatively
detach that power-producing pattern of the voltage (the sinusoidal ripple
exemplified by curve 3 in Fig.2, just to show that it is no more related
to the offset in the way it appears on the screen of the oscilloscope.
The home of that power-producing pattern of the voltage is elsewhere.
Of course, its home must be somewhere on the x-axis, because, as seen,
it is the momentary values of the voltage wiggling around an axis that
are the values which matter for the calculation of power. The x-axis,
which is at the zero of the y-axis, provides the best reference level
to know the true values of voltage which are to be used for the average
input power 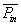 calculation.
calculation.
Current-producing pattern of voltage is either one
of the curves 1 or 3 in Fig.2 and Fig.3. Notably, they produce the same
current‒‒curve 2. Trivially, the current-producing and the
power producing patterns of voltage overlap each other for voltage which
has no offset (curve 1 in Fig.2 and Fig.3).
Remarkably, for voltage with offset the current-producing
pattern and the power-producing pattern of the voltage do not overlap
each other because of the specific but physically correct way the constant
voltage offset is to be eliminated from the instantaneous voltage values
when voltage has offset, so that these instantaneous voltage values become
appropriate for correct average input power calculation in the instances
when voltage has offset.
But where exactly on the x-axis must the power-producing
pattern of the voltage, which is derived from the voltage with offset,
be positioned?
Indeed, once we understand that voltage offset has
no contribution to power and therefore must be eliminated from the instantaneous
values of voltage seen on the screen of the oscilloscope, so that these
corrected voltage values can be used for correct calculation of input
power, the crucial question becomes how this elimination of the pesky
constant voltage offset is really to be done.
One obvious, although wrong proposal, may be to eliminate
the offset of the voltage by just bringing the voltage trace (curve 3
in Fig.2 and Fig.3) vertically downwards, respectively, upwards for a
negative offset, back to its non-offset reference position (curve 1 in
Fig.2 and Fig.3). It is immediately evident, however, that this way of
eliminating offset ignores the physical fact that at time t = 0
the capacitor has an actual non-zero voltage, F, applied to it.
In other words, if this way of eliminating offset is adopted, the initial
point denoted as A; namely, the point at t = 0, of the offset voltage,
will not belong to the time-varying part of the actually applied voltage
any more. However, it must belong.
Only the product of the current at time t = 0
by the actual non-zero voltage applied at time t = 0 gives the
correct power value. Indeed, it should go without saying that the real
voltage value at t = 0, where point A is positioned, should be
used in calculating the power and the only thing necessary is to somehow
remove offset for the rest of the wavy voltage curve.
The only trace which can both possibly retain the
pattern of time-varying part of voltage while at the same time lose its
constant offset and have the point A belong to it, is the non-offset voltage
trace 4 in Fig.2 and Fig.3. This new, power-producing voltage curve is
phase-shifted with respect to the original voltage trace 1 in Fig.2 and
Fig.3. Notice, the phase-shift of the newly obtained voltage curve 4 with
respect to voltage curve 1 renders also a new phase-shift of that newly
obtained voltage curve 4, used to correctly calculate average input power,
and current curve 2. Thus, the new phase-shift between curves 4 and 2
is different from the natural phase shift between curves 1 and 2 (respectively,
the same natural phase shift between curves 3 and 2), seen in every college
level textbook on that subject matter.
In this illustration one sees clearly why the power-producing
pattern of the voltage, derived from the voltage curve 3 with offset in
Fig.2 and Fig.3, is phase-shifted with respect to the original no-offset
voltage curve 1 in Fig.2 and Fig.3.
Obviously, the offset provides a substantial advantage
because at t = 0 it already ensures the level of charging of the
capacitor, which for the voltage curve without offset (curve 1 in Fig.2
and Fig.3 occurs later in time, requiring energy input to reach the same
level of charging.
It should be appreciated that offset insures the fortunate
circumstance that the capacitor is already charged as early as time t
= 0. That charge is served on a platter, earlier than it would be
acquired if the charging has started from an uncharged capacitor. The
capacitor, being already charged at time t = 0, allows for the
further run of the voltage curve, after t = 0, to proceed, having
the same shape as the shape of the curve that started from uncharged capacitor.
That shape which proceeds from the already charged level at t = 0
will be built earlier than the same curve for the uncharged
capacitor.
Notice, the phase-shifted voltage trace 4 in Fig.2
and Fig.3, comprising the power-producing pattern of the voltage, following
from the voltage curve with offset, is not voltage which current is derived
from. The shown phase-shifted voltage trace only provides the correct
voltage values, which the corresponding values of current must be multiplied
by, so that correct input power values can be obtained, in consideration
of the fact that the applied voltage has offset.
Therefore, if the actually applied voltage is 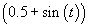 ,
that voltage must be changed, in accordance with what was just said, to ,
that voltage must be changed, in accordance with what was just said, to
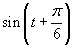 in
order for the average input power in
order for the average input power 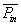 to
be calculated correctly through integration. to
be calculated correctly through integration.
Therefore, if input power 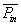 is
to be calculated correctly when voltage has offset, the corrected mutual
disposition of current and voltage is to be as it is exemplified in curve
2 with respect to curve 4 in Fig.2 and Fig.3, instead of mere shifting
of the voltage to eliminate the offset (curve 1 in Fig.2 and Fig.3). is
to be calculated correctly when voltage has offset, the corrected mutual
disposition of current and voltage is to be as it is exemplified in curve
2 with respect to curve 4 in Fig.2 and Fig.3, instead of mere shifting
of the voltage to eliminate the offset (curve 1 in Fig.2 and Fig.3).
Correct calculation of input power requires that the
wave with offset be represented by the same wave without offset but phase-shifted.
The offset 0.5 is replaced by change of sine argument t.
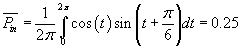 (3)
(3)
Similar are the arguments in the case when the voltage
offset is negative
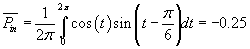 (4)
(4)
Notice again, the phase-shifting of voltage is done only to have the
correct momentary products of V(t) times I(t) and does not
mean that a discrepancy in the timing of the current and voltage is introduced.
Under the integral the phase-shifting of the voltage only transports the
correct voltage value, mindful of its offset, to coincide properly with
the current. In other words, in the long run, offset translates as a phase
shift of the non-offset voltage when calculating power correctly.
When the offset F is equal to the amplitude of the sinusoidal
voltage, then the voltage used to calculate power is so phase-shifted
with respect to the original voltage (trace 1) that its phase coincides
with the phase of the current.
The offset can be greater than the amplitude of the applied sinusoidal
voltage pattern (cf. trace 1, which exhibits the pattern). In such a case,
the voltage values used to calculate power will be further phase-shifted
with respect to the original voltage (trace 1), in addition to the 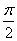 phase shift, corresponding to the offset equaling the amplitude of the
sinusoidal current, F = Vm. Finally, the values of the original
voltage trace (trace 1) can be used to calculate power correctly when
the offset becomes F = 4Vm. For F > 4Vm the picture
repeats itself, a point, corresponding to F = 4.5Vm, being
the same as point A in Fig.2, as an example.
phase shift, corresponding to the offset equaling the amplitude of the
sinusoidal current, F = Vm. Finally, the values of the original
voltage trace (trace 1) can be used to calculate power correctly when
the offset becomes F = 4Vm. For F > 4Vm the picture
repeats itself, a point, corresponding to F = 4.5Vm, being
the same as point A in Fig.2, as an example.
Especially interesting is the case when the offset is negative, say,
F = -0.5 and the voltage has the form 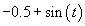 ,
as trace 3 in Fig.3. Then, ,
as trace 3 in Fig.3. Then,
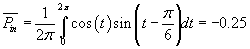 (4)
(4)
As explained above, when under the integral, the instantaneous current
must be multiplied by the numerical value of a properly phase-shifted
voltage. Otherwise the integral obliterates the offset of the voltage,
causing the current to be multiplied by the wrong voltage value, unaffected
by the fact that said voltage has offset.
As seen from eq.(4) , instead of a positive value (when a dissipative
element R is present) or a zero, which is the usually known result of
integrating power in passive circuits, the value of the integral is negative.
This means that the action of the generator in this illustration is to
return energy to the generator while producing energy; namely, Joule heat
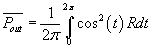 , (5) , (5)
on the dissipative element R, no matter how negligible. In other words,
to produce energy per unit time, the generator not only does not spend
energy but has energy returned to it. This is an outright violation of
conservation of energy due to inherent asymmetries in electrical systems,
in fact, the ultimate violation of CoE.
To avoid confusion, it should be recalled also that standard literature1-4
requires that the power balance be carried out only for the power coming
into and out of the electric circuit. The power needed to run the generator
is not included in the power balance. Therefore, it is not a requirement
for violating CoE to demonstrate a self-sustaining system, powered by
the excess power produced at the output.
The general conclusion is that any time there is a DC voltage offset,
together with AC voltage, there is a violation of conservation of energy‒‒either
by the obtainment of more or the obtainment of less energy than the energy
put into the system. This conclusion is in harmony with other observations
of this author of CoE violation, whereby energy produced does not come
from a previously existing energy reservoir but comes about due to saving
from the input as a result of favorable juxtaposition of the elements
of the system and its construction.
Obeying of CoE in electrical systems when continuous signals are applied
is only an exception. CoE in such cases is abided by only when when F
= 0 or, in general, when the elements of the circuit are only active
(dissipative).
Of course, the same analysis and conclusions hold also to more complex
forms of the applied voltage such as sinusoidal signals containing higher
harmonics as well as periodic signals other than sinusoidal. The above
analysis provides an opportunity to look for greater effects showing more
expressed violation of CoE.
It should also be obvious that when the circuit consists of only active,
dissipative, elements, such as resistors, not only will there be no natural
phase shift between current and voltage at any F value but there
will be no phase shift between the applied voltage with any F and
the voltage value used for the power calculation according to the above
considerations. When there is a non-zero F in the voltage applied
on a resistor, current will, symmetrically, also have an offset. Thus,
in this case of active resistance, the offset in voltage causes offset
in current and these offsets (in voltage and current) should be included
in the calculation of power. Therefore, in this case, the correct power
value is equal to the product of the actually applied instantaneous current
and voltage. In the case of an active resistance, there is no natural
asymmetry between current and voltage of the type described above and
therefore there will be no violation of CoE due to phase-shifting of voltage,
used to calculate power with respect to its actually applied value, as
in the above case of passive elements. Violation of CoE in the case of
active resistance may be sought along the lines of the discrepancy in
the treatment of discrete, finite number of values within a period, not
discussed here, or by looking for other asymmetries also not under consideration
in this text.
Purely electric methods, even just purely theoretical, of verifying the
reality of the above effects are quite sufficient, provided the described
correct method of determining input power 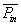 is applied.
is applied.
It is to be emphasized again that when voltage offset is negative the
average input power 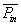 has
a negative value. This means, as already pointed out, that average output
power has
a negative value. This means, as already pointed out, that average output
power 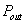 has been
produced at no expense of input power, all the power from the generator
being returned back to it. This is the ultimate violation of conservation
of energy, when power has been
produced at no expense of input power, all the power from the generator
being returned back to it. This is the ultimate violation of conservation
of energy, when power
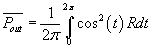 (5) (5)
on the resistor of the RC-circuit is produced by saving of all of the
input power, all of the input power being even returned back to the generator.
Thus, the generator causes the RC-circuit to become a power source returning
power---negative integral of $I V$ over the period. At the same time,
power of the amount of
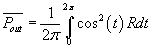 (5) (5)
is produced in the RC-circuit. This is power dissipated on its active
resistor, denoted by R.
Although calculation of input power is more exact by using integrals,
as we have done here, not the least because in this way input power of
more complex signals can be calculated, usually, for simplicity and convenience,
standard texts calculate the average input power of sinusoidal signals
by calculating the root mean square values (rms values) of the voltage
and current and multiply that product by the cosine of the natural phase-shift
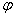 between voltage
and current. between voltage
and current.
In view of what was discussed herein, the correct calculation of input
power using rms values must be done by multiplying the product of these
rms no-offset voltage and current values by the cosine of a phase-shift
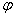 ', different
from the natural phase-shift ', different
from the natural phase-shift 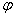 ,
as explained earlier. ,
as explained earlier.
In another publication of this author, violation of energy conservation
is presented when electrolysis of water is carried out in an undivided
electrochemical cell. This is the most important effect, so far unaccounted
for, in the widely discussed phenomenon known as “cold fusion''.
Although ideologically, every example of violation of conservation of
energy is equally significant, conservation of energy violation in electrical
circuits, discussed above, seems to be of especially great importance
because it does not involve moving parts or messy chemicals. It also insures,
as said, the ultimate violation of energy conservation, allowing production
of energy without any energy input whatsoever. This is the reason why
exactly the violation of energy conservation in electrical circuits, having
direct and immediate practical applicability by one skilled in the art,
was chosen for patent protection.
The big novelty in the discussed way of producing energy is that the
energy produced in the way discovered here does not come at the expense
of depleting of a previously existing energy reservoir. This is not an
alternative source of energy, as it is understood nowadays, involving
solar, wind and other energies, which utilize already existing energy
by converting from an already existing form into a form to be used for
some concrete practical purposes. The energy discussed here is not even
alternative in the sense Tesla implies the term, because in Tesla's proposals
the energy produced, in no matter how exotic a way according to contemporary
science, is still energy from a previously existing energy reservoir.
The energy obtained according to this discovery, alternatively called
excess energy or “energy out of nothing'', does not come about
at the expense of a pre-existing (already existing) energy reservoir.
Excess energy in this discovery is produced as a result of saving from
the input energy due to so far unrecognized favorable juxtaposition and
interaction of real elements and factors, other than already available
energy. Thus, the phrase “production of energy out of nothing''
is only a figure of speech. It is only a way of expressing that there
is no pre-existing energy reservoir. It does not mean that there are no
other existing real non-energy components and factors, and their respective
interactions, which are due to the approach described herein. In their
totality, they allow for the production of energy, despite the absence
of such energy prior to commencing the process. As already said, the method
is based on utilizing natural asymmetries, so far unrecognized for “production
of energy out of nothing'', which exist in standard classical physics,
and concretely here, in the classical theory of electricity.
It should also be strongly and specially emphasized that input power
in electrical circuits, such as the one discussed here, is never measured
directly. What is measured directly are two non-power, non-energy quantities,
namely, voltage and current, which are then subjected to mathematical
calculation to obtain input power. Input power in circuits at hand is
always only obtained indirectly, through calculation. The fact that electric
power in such circuits is never measured directly but is always determined
indirectly, through calculation, makes the method of calculation crucial
for the validity of power determination in electrical systems at hand.
Also, the fact that power in circuits, such as the one observed, is always
calculated from the direct measuring of two non-power, non-energy, quantities;
namely, current and voltage and is never measured directly, has a crucial
bearing on the ruminations about the practical applications of the new
phenomenon, discussed here.
Thus, the experimental proof for the reality of the above discovery consists
in the correct, well understood, experimental determination of voltage
and current, obtained in the concretely described way here, and their
correct mathematical handling, also described herewith. The novelty of
this proposal with clear practical application lies is the combination
of these factors.
Thus, the experimental proof for the reality of the above discovery consists
in the correct, well understood, experimental determination of voltage
and current, obtained in the concretely described way here, and their
correct mathematical handling, also described herewith. The novelty of
this proposal with clear practical application lies is the combination
of these factors.
Violation of conservation of energy in mechanical systems, as well as
in electrochemical systems, is demonstrated in more detail elsewhere.
All demonstrated possibilities to violate conservation of energy make
it impossible to consider conservation of energy as a scientific
principle any more. This discovery of the so far unrecognized inherent
possibility to violate conservation of energy opens unforeseen, far-reaching
perspectives for the building of principally new energy generators, as
well as an ideological change in all of science. It changes the way science
views energy. Such ideological change is probably of even greater importance
than the pure utilitarian applications of the discovery at hand. It frees
science from the artificially imposed limitations and strangulations set
forth by the requirement to think of energy as something pre-determined.
The discovery discussed causes a complete overhaul of the simplistic way
science perceives energy and distinguishes it from quantities which are
necessarily conserved, such as, a given mass of a given unique, single
body in a given system or the absoluteness of time. Uniqueness of mass,
absoluteness of time, as well as other problems, explicitly or implicitly
disregarded in contemporary physics, will also be discussed elsewhere.
From the above, it has become clear that it is inevitable to apply a
hitherto unknown method, described above, of correct calculation of the
average input power when applying alternating voltage having constant
voltage offset to a particular electric circuit containing reactive elements.
References
1. Panofsky W.K.H. and Phillips M., ClassicalElectricity and Magnetism, 2nd ed.,
Addison-Wesley, Reading, MA,1962.
2. Jackson J.D., Classical Electrodynamics, 2nd ed., John Wiley&Sons, NewYork,1975.
3. Purcell E.M., Electricity and Magnetism, Berkeley Physics Course, Volume 2, McGraw Hill, New York, 1985.
4. Fowler R.J., Electricity. Principles and Applications, p.202, McGraw Hill, New York, 1985.
Author's email:
:
navitasexnihilo@hotmail.com
|